Yanpu/ Lesley

Yanpu/ Lesley

Logistics Regression VS SVM

Published:

Similarities

Both logistic regression and svm is used for classification (svm can also be used for regression); and have linear seperable decision boundary (kernel can also be added in logistic regression). Logistic regression and svm are highly related, we can try to change the form to derive svm by using a logistic regression model.

For a two-class problem:

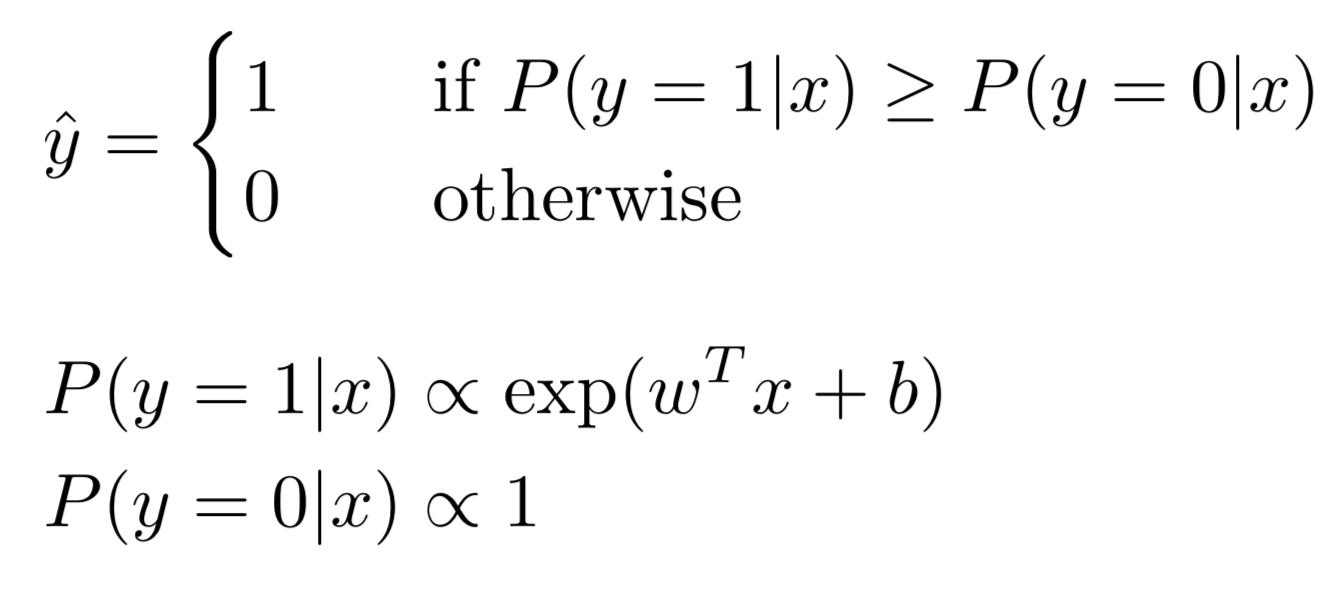
If we change the probability output of logistic regression into class, by setting a constraint on the likelihood ratio: p(y=1|x)/p(y=0|x) >=c, c>0, take log of both sides: log(p(y=1|x)) -log(p(y=0|x)) >=log(c), put the origin definition back: wTx +b >= log(c), we pick c to make log(c) =1, and put a quadratic penalty on the weights, then we can get

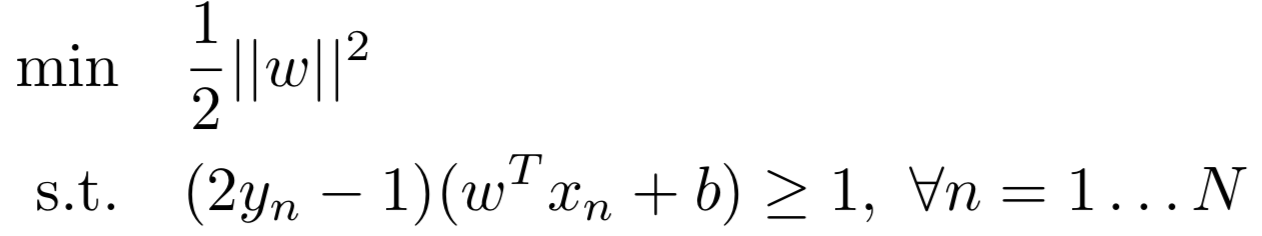
Differences

Let’s list the loss functions here to tell the differences between LR and svm.

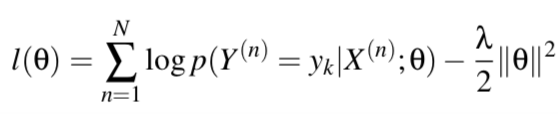
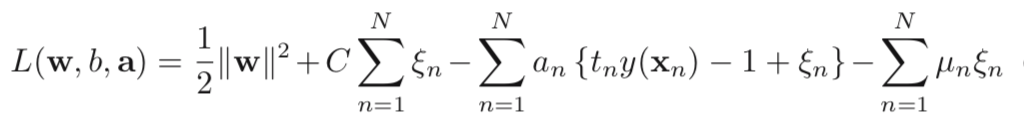
Logistic regression tries to maximize the probability of data, and it works on the whole training data. LR wants to make sure the data is as much further away from the decision boundary as possible. Svm constructs a hyperplane which is obtained by maximizing the margin. This margin is defined by a small amount of data (support vectors), and these support vectors are the points closest to the decision boundary. In turn, if there are outliers in the training set, it may generate a totally wrong hyperplane. Based on above principles, let’s make comparison between LR and svm from different aspects.

Data: As svm is mainly determined by a small group of data, it will be more sensitive to outliers. As for LR, it will perform badly, if the whole dataset is strongly unbalanced. Also, compared to LR, svm is more fit for small dataset with multiple features.

Non-linear seperation: svm will tend to use kernel, as it can product the data into higher dimension and try to find a linear seperation in that space. Again, as only a few points (support vectors) will be involved, the cost won’t be too high. On the contrary, LR will avoid using kernel. Because all the dataset need to be calculated to find the decision boundary.

Overfitting: L2 regularization is kind of included in svm’s loss function, together with the parameter C, both of them can play a role in controlling the trade-off between minimizing training errors and model complexity.

Output: LR gives probability output, which is better to measure the confidence of the prediction.

Reference

[1]. http://www.mamicode.com/info-detail-517504.html

[2]. https://compbio.soe.ucsc.edu/genex/genexTR2html/node3.html

Leave a Comment

You May Also Enjoy

Quick Notes: Variation of GAN (Stacked GAN, StackGAN++, PA-GAN)

Published:

For the past 4 months, I have been working on cardiovascular disease risk prediction. Through this, I come up with an idea to utilize GAN to learn in a progressive way and decide to write a paper on this topic(Sry, I can’t talk much about my idea in details). Then, I began doing background research and found three related topic. In this post, I will give summarizations of these topic.

Quick Notes: Useful Terms & Concepts in NLP: BOW, POS, Chunking, Word Embedding

Published:

NLP algorithms are designed to learn from language, which is usually unstructured with arbitrary length. Even worse, different language families follow different rules. Applying different sentense segmentation methods may cause ambiguity. So it is necessary to transform these information into appropriate and computer-readable representation. To enable such transformation, multiple tokenization and embedding strategies have been invented. This post is mainly for giving a brief summary of these terms. (For readers, I assume you have already known some basic concepts, like tokenization, n-gram etc. I will mainly talk about word embedding methods in this blog)

Quick Notes: Summarization about Current NER Methods in Deep Learning

Published:

Recently, I have been working on NER projects. As a greener, I have spent a lot of time in doing research of current NER methods, and made a summarization. In this post, I will list my summaries(NER in DL), hope this could be helpful for the readers who are interested and also new in this area. Before reading, I assume you already know some basic concepts(e.g. sequential neural network, POS，IOB tagging, word embedding, conditional random field).

Useful Concept for Medical/Healthcare Data Risk Prediction

Published:

This post is for explaining some basic statistical concepts used in disease morbidity risk prediction. As being a CS student, I have found a hard time figuring out these statistical concepts, hope my summary would be helpful for you.