Ensemble learning: Stacking
Published:
Stacked generalization, stacking, is composed of two types of layers:
- base classifiers (generally different learning algorithms)
- meta learner (tries to combine the output of the first layer to obtain the final results)
To maintain the performance of a stacking model, it requires diversity and accuracy among each classifiers. Because by applying similar models, it is highly possible that they would make wrong decisions at the same instance. However, if the classifiers are diverse, their errors will not be highly correlated, and the combination of classifer will perform better than the base classifiers.
Before explaining stacking algorithm in details, I’d like to make a horizontal comparison of stacking against bagging and boosting. As these three algorithms all belong to ensemble learning, which is to combine a set of classifiers together with their outputs such that the result outperforms all the individual classifiers. Here, I have listed the differences in the table below.
Table 1
| Method | Goal | Data Partition | Classifiers | Combination of base models |
|---|---|---|---|---|
| Bagging | decrease variance | sampling with replacement | same type & parallel ensemble | average |
| Boosting | decrease bias | emphasize training instances, previously mis-classified | same type & sequential ensemble | weighted majority vote |
| Stacking | both | CV (generally LOOCV) | diverse types & two layers (base, meta) | meta learner |
Stacking Algorithm
Given dataset D, T base learners, firstly partition into K equal-size subset datasets, similar to K-fold CV process, then,
- Step 1: Prepare input, learn base classifiers
- input: for each base learner, use (D - Di) as training set and Di as testing set
- base model generation
- Step 2: Constructing training set for meta learner, learn meta model
- creating training data over Di: the output predicted labels from level-0 are kept as new features; thus, at the end of this stage, it will contain T attributes, and keep the original class labels as labels in new data
- meta model generation
- Step 3: Regenerate base learners on the whole dataset D
- for each learner, it has previously worked on all K subsets in Level-0, generating K fits; so D will be runned on these K fits, and finally average the results, this is the test data for meta learner (it is expected that the classifier will be slightly more accurate)
Details are shown in Fig. 1 and Fig. 2.

Figure 1. Stacking Algorithm
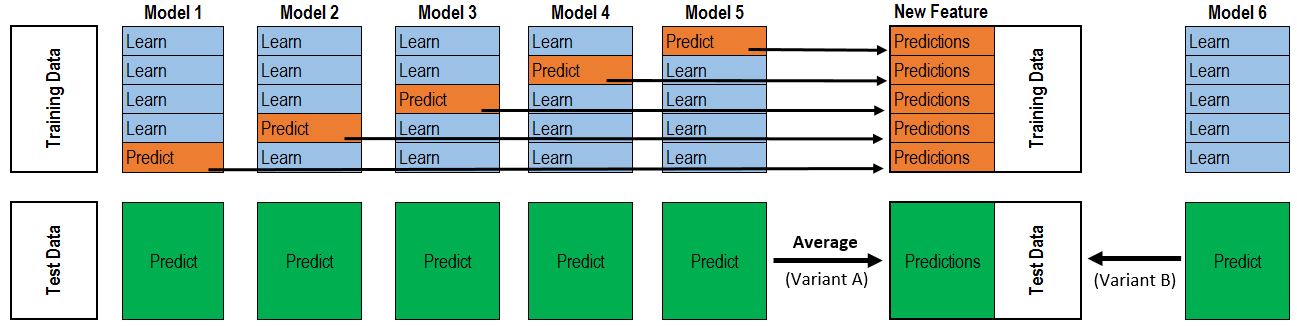
Figure 2. Partial Framework
**Attention** In Fig. 1, the algorithm works on the wholde dataset to regenerate base models. Alternatively, you can try to split D into training and testing set at the very beginning. Conduct step 1 and step 2 on training part, then regenerate base models only on testing set. One advantage is it can be less time consuming, as it doesn't need to work on the full data. Fig. 2 is a good example to directly show how stacking works. However, in the upper blue section (Training Data), it's a little bit confusing. You may mistakenly think that 5 models seperately work on 1 fold (Predict) and 4 folds (Learn) only once, which is Model 1 predicts on the 5th fold, Model 2 predicts on the 4th fold and so on so forth. In fact, take Model 1 for example, it need to do prediction on all each single fold, and learn from every four folds from the full data.
class Stacking(object):
def __init__(self, seed, n_fold, base_learners, meta_learner):
self.seed = seed
self.n_fold = n_fold
self.base_learners = base_learners
self.meta_learner = meta_learner
self.T = len(base_learners) # num of base learners
def generateBaseLearner(self, X_tr, y_tr, X_te, y_te):
n1 = X_tr.shape[0]
n2 = X_te.shape[0]
kf = KFold(n1, n_folds= self.n_fold, random_state= self.seed)
#constructing data for meta learner
meta_train = np.zeros((n1, self.T))
meta_test = np.zeros((n2, self.T))
for i, clf in enumerate(self.base_learners):
meta_test_i = np.zeros((n2, self.n_fold))
for j, (train_index, test_index) in enumerate(kf):
X_train = X_tr[train_index]
y_train = y_tr[train_index]
X_holdout = X_tr[test_index]
y_holdout = y_tr[test_index]
clf[1].fit(X_train, y_train)
y_pred = clf[1].predict(X_holdout)[:]
print 'Base Learner:%s accuracy = %s' % (clf[0], metrics.accuracy_score(y_holdout, y_pred))
# filling predicted X_holdout into meta training set
meta_train[test_index, i] = y_pred
meta_test_i[:, j] = clf[1].predict(X_te)[:]
meta_test[:, i] = meta_test_i.mean(1)
self.meta_learner.fit(meta_train, y_tr)
y_result_pred = self.meta_learner.predict(meta_test)
print 'Final accuracy = %s' % (metrics.accuracy_score(y_te, y_result_pred))
return y_result_pred
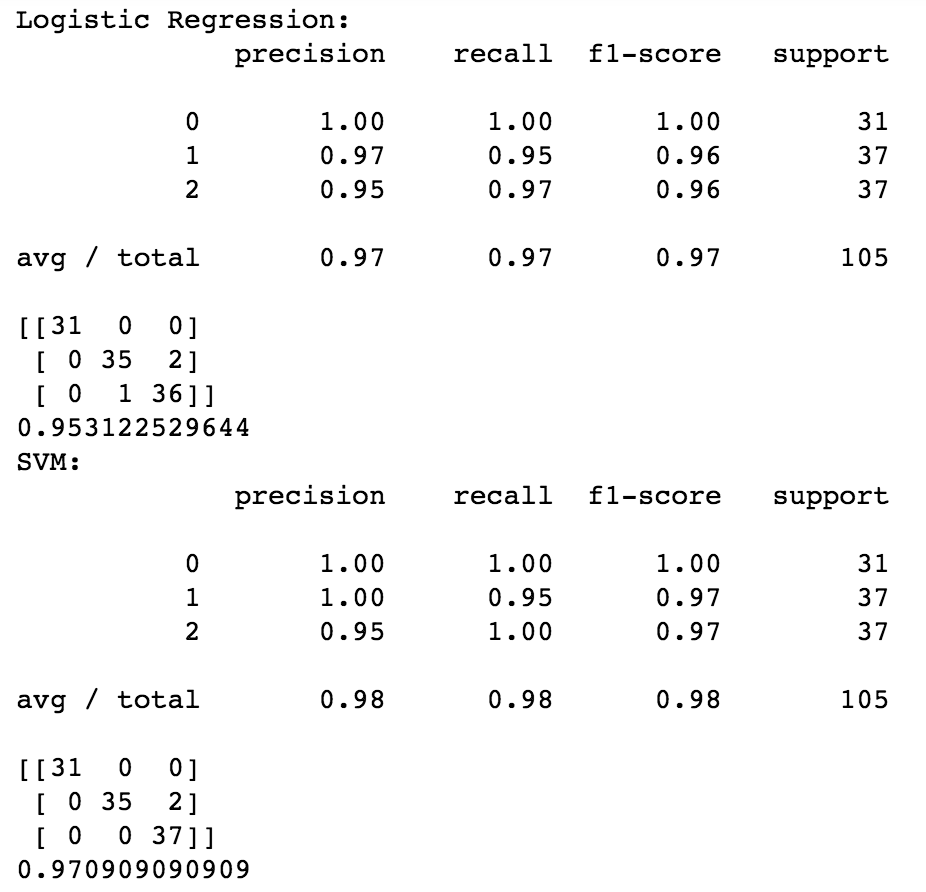
Figure 3. Stacking Implementation
Experiment
dataset: iris data; base learner: SVM, Random Forest, KNN; meta learner: Logistic regression; Fig. 3 shows classification report, confusion matrix for training set, and accuracy for testing set. For each individual base classifier, SVM performs better than the other three. Then, I use SVM as meta learner, the other three as base ones. The testing accuracy is 0.977, which is better than all these 4 individual learners. The reason behind this is in Fig. 3, we can tell that random forest makes some mistakes on class3 instances, logistic regression has other mistakes on class2 and 3 and knn has no mistakes(remember these mistake instances are from training set). So when combining them together, certain mistakes made by one classifer can be counteracted by the correct identification from other classifiers.

Questions about Stacking
Though it is not hard to understand the principle of a stacking model, there are still a bunch of questions need to be answered.
- Base Learner
- how many models
- which models to use
- what kind of parameters
- Meta Learner
- which model to use
- what kind of parameters
- number of attributes
About the number of base learners: it is a trade-off situation. On one hand, it is beneficial to learn from a large group (meta learn learns from base classifers). On the other hand, increasing number of level_0 will make the task more time consuming. Also, if you enlarge level_0 by adding similar models, it probably will not enhance the performance.
About which models to use in Level_0, let’s conduct a set of experiments. From Fig. 4, we know that SVM has the best performance on training and testing set, then comes with lg and knn, rf ranks as the last one. So I have tried to make different combinations of these four models to see the results.
Table 2
| Base Learner | Meta | Accuracy: training, testing |
|---|---|---|
| [svm, lg, knn] | rf | 1, 1 |
| [svm, rf, knn] | lg | 1, 1 |
| [svm, lg, rf] | knn | 1, 1 |
| [knn, lg, rf] | svm | 0.98, 0.97 |
In general, all these four groups did a pretty good job. Only the 4th ranks a little behind. About group 1 to 3, they all have relatively strong base learners, especially svm. It seems for stacking it’s more important to have accurate base learners than meta learner. After all, meta learner learns from the predictions made from each base learner. So, I tried to replace meta learn in group 1, 2, 3 to gnb (GaussianNaiveBayes, whoes performance is even worse than rf in this case). Unsurprisingly, the accuracy remains the same. However, this conclusion doesn’t mean meta learner is not significant. For group 1, though it has strong base learner, its meta learner is the weakest. I have tried to change the random_state for all the models, then at some points, the accuracy decreases (though the accuracy of each base learner keeps the same).
The above conclusion is not absolutely true. Because there are some defects in these experiment.
- The size of this dataset is very small, only 150 pieces of record. So there are not enough training set for the classifiers to learn, and also not enough testing data to prove the performance of our models. Like for Table 2, the value of n_fold for all the groups is 3. If I increase it to 5 (meaning more training data), then the accuracy of the 4th group also increases to 1.
- Lacking appropriate model to do the experiment. For example, when evaluating the importance of base learners, I should also construct contrasting experiments, which is replacing the original base leaner set in group 4 with stronger models (the ones better than svm), to see if the accuracy would increase. But I haven’t found models better than svm, so I skipped this procedure.
What kind of models should be used as meta learners? Let’s go back to the Level_0, the base learners: in this stage, the goal is to utilize various classifiers to learn from the dataset, and generate predictions(which is more directly ) to be used as input for level_1. In level_1, the goal is to combine all these different sets of predictions together, to summarize correct information. Remember, compare to the original attributes, these predictions are more intuitive. So there is no need to use complex models as meta learner. In turn, these models may even increase the probability of overfitting.
The number of attibutes should be included in meta learner: in some related papers, it is suggested to also including original features as input for meta learner. However, these predictions are made based on attibutes. It means include too many original features may also cause overfitting. Thus, maybe it’s better not to add these attributes.
Reference
[1]. Wolpert, D. H. (1992). Stacked generalization. Neural Networks, 5(2), 241-259. doi:10.1016/s0893-6080(05)80023-1
[2]. Sesmero, M. P., Ledezma, A. I., & Sanchis, A. (2015). Generating ensembles of heterogeneous classifiers using Stacked Generalization. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 5(1), 21-34. doi:10.1002/widm.1143
[3]. Ledezma, A., Aler, R., & Borrajo, D. (n.d.). Heuristic Search-Based Stacking of Classifiers. Heuristic and Optimization for Knowledge Discovery, 54-67. doi:10.4018/978-1-930708-26-6.ch004
[4]. Aggarwal, C. C. (2015). Data classification: algorithms and applications. Boca Raton: CRC Press.
[5]. http://blog.kaggle.com/2016/12/27/a-kagglers-guide-to-model-stacking-in-practice/
[6]. https://zhuanlan.zhihu.com/p/32896968


Leave a Comment