Notes of Recommendation System
Published:
When building a recommendation system, it mainly deals with problems, such as: How to collect data (known ratings) in the utility matrix; How to estimate unknown ratings from the known; Evaluating approach
Dataset
There are two types of entities, users and items. A utility matrix is used for storing each user-item pair, and it is usually a sparse matrix. This is because most people haven’t rated most items, new items have no ratings, or new users have no history information.
Based on these features, there are mainly 2 groups of architechtures to build a recommendation system: content-based and collaborative filtering. In this post, I mainly focus on talking about these two approaches.
Content-based
- Main idea: focus on item properties, recommend items to customer x, which is similar to previous items rated highly by x
- Example: recommend movies with same actors
Item Profile In content-based system, an item profile must be created for each item, recording important properties of that item. For text content, we can use TF-IDF to calculate scores for the document to create doc profile, and pick the words with highest scores as important features. wj = (w1j,…,wij,…,wkj)
For images, one way is to let the users making tags for each pictures. However, users may not be willing to do this, as it is very troublesome.
User Profile It is used for describing the users’ preferences. It can be created into 2 ways.
- weighted average of rated item profiles
- variations: weight by difference from average rating for item. Given user profile wx, item profile wj:
rxj = cos(wx, wj) = wxwj / ||wx||.||wj||
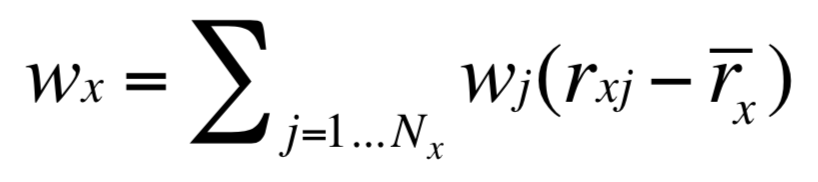
Table. Pros & Cons for Content-base System
| Pros | Cons |
|---|---|
| no need for data on other users | hard to choose proper features |
| able to recommend to users with unique tastes | hard to create user profile for new users |
| able to recommend new unpopular items | never recommends items beyond user’s content profile |
| can provide explanations (item features) | unable to exploit quality judgements of other users |
Collaborative filtering
Main idea: focus on harnessing quality judgements of other users, it includes 2 process, finding users having similar tastes, and recommending what the similar users like.
Find Similar Users: rx: the vector of user x’s ratings
- Jaccard distance: ignore ratings, only focus on which items have been rated,
- Cosine distance: problem: it will tread missing ratings as negative. Sim(x,y) = cos(rx, ry) = rxry||rx||.||ry||
- Pearson correlation coefficient:
Sim(x,y) = cos(rx, ry) = (rx-rx,avg)(ry-ry,avg)||rx-rx,avg||.||ry-ry,avg||
Example:
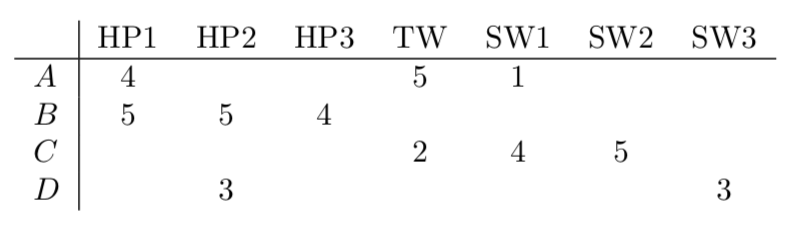
Figure 1. Utility Matrix
| Method | (A,B) | (A,C) |
|---|---|---|
| Jaccard | 1/5 | 2/4 |
| Cosine | 0.38 | 0.322 |
| Pearson | 0.092 | -0.559 |
Intuitively, we want sim(A,B) > sim(A,C). Because both A,B have a high rating for HP1, and A,C have two polar ratings for TW and SW1. However, by using Jaccard distance, it returns the values showing C is more close to A, rather than B. This tells us that Jaccard is less suitable for the case with detailed ratings. Instead, it only cares if the item has been rated. Cosine distance is kind of better than Jaccard. But it still can’t significantly tell the difference between (A,B) and (A,C). This may be caused by the ‘negative’ missing ratings. Finally, by normalizing ratings with average scores, Pearson coefficient has remarkably tells these two groups apart.
User-User Collaborative Filtering: For user u, find similar users, estimate rating for item i based on ratings from similar users
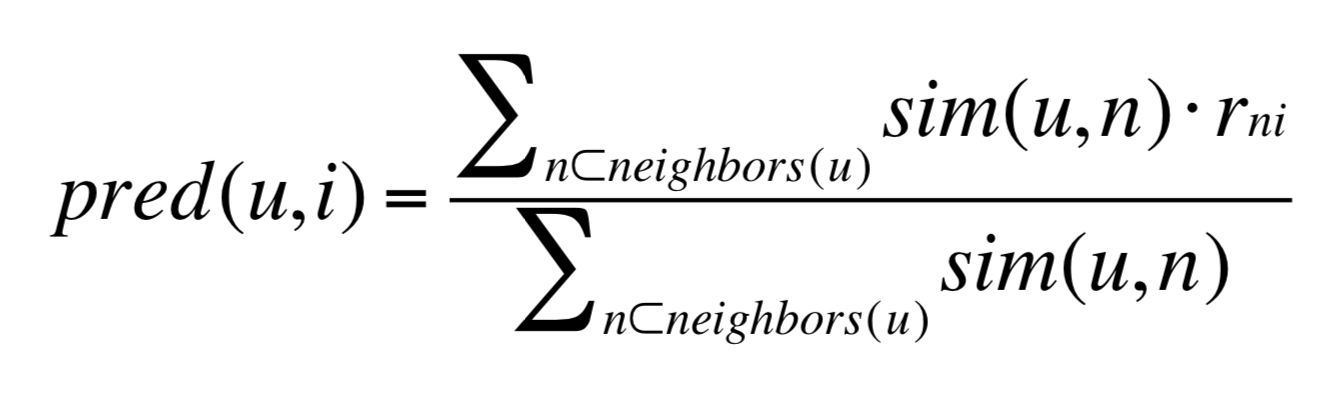
Item-Item Collaborative Filtering: For item i, find other similar items, estimate rating for i based on similar items. Sij denotes similarity between item i and j, rxj denotes ratings of user x on item j, N(i;x) represents set of items rated by user x, similar to item i
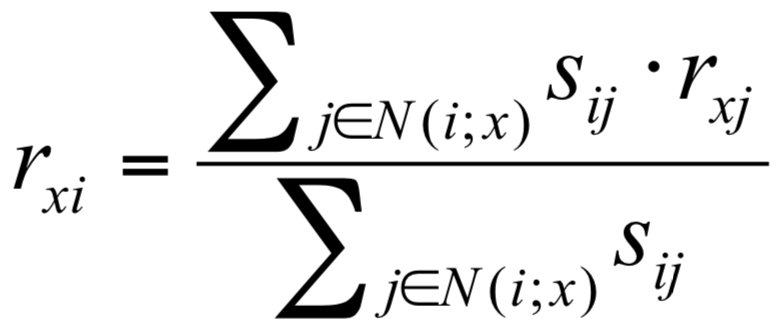
Example:
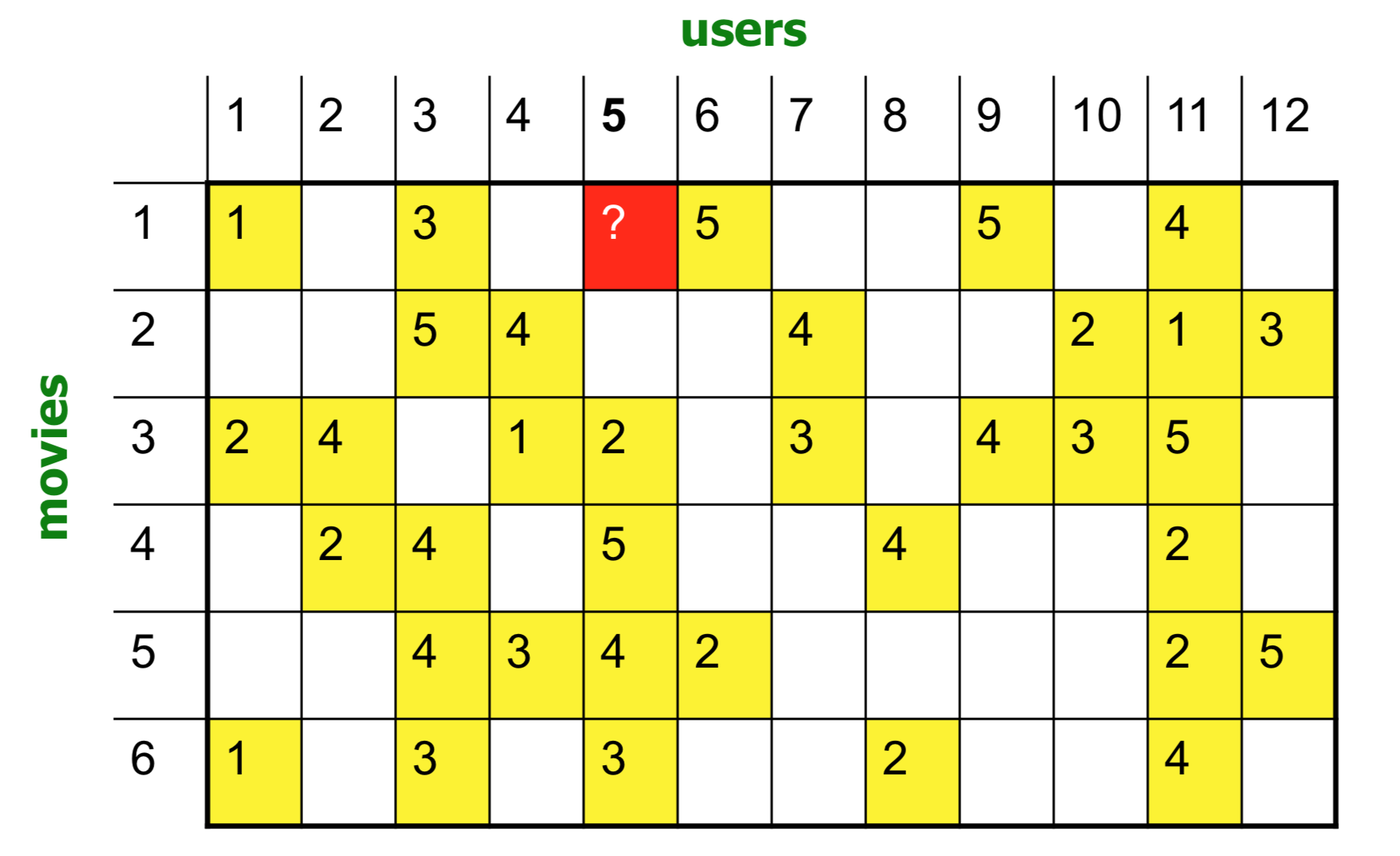
Neighbor selection: Identify movies similar to movie 1, rated by user 5, I choose movie 3 and 6; Substract mean rating mi from each movie i: m1 = (1+3+5+5+4)/3.6, row1:[-2.6, 0, -0.6, 0, 0, 1.4, 0, 0, 1.4, 0, 0.4, 0]; compute cosine similarities among rows: sim(1,m) = [1, -0.81, 0.41, -0.1, -0.31, 0.59]; Prediction: r1,5 = (0.41*2+0.59*3)/ (0.41+0.59) = 2.6
Tips: In practice, it has been observed that item-item CF often works better than user-user. This is because items are simpler, users may have multiple tastes.
Table. Pros & Cons for Collaborative Filtering System
| Pros | Cons |
|---|---|
| works for any kind of item, no feature selection needed | need enough users in the system for matching |
| the matrix is sparse, hard to find users that have rated the same items | |
| can’t recommed items that haven’t been rated before | |
| can’t recommend items to users with unique taste, meaning it tends to recommend popular items |


Leave a Comment